About the PROBLEM #2 ("икки") from International Olympiad "TUYAMAADA" 2021 - Junior League

           See link, obtained from www.molympiad.net.

          We will formulate the following related problem:

 

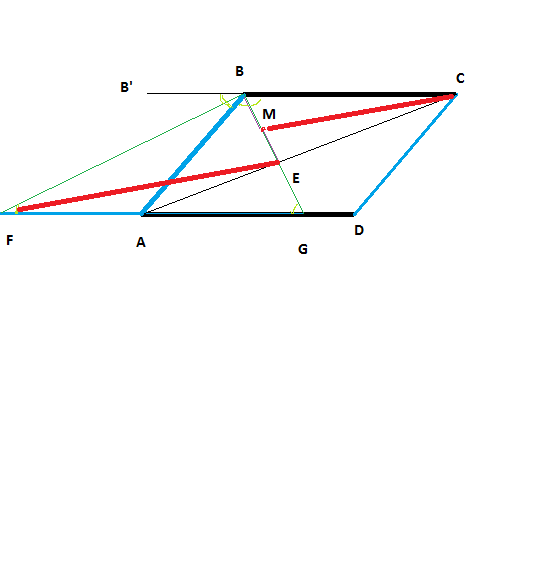
"The bisector of angle $B$ of a parallelogram $ABCD$ meets itd diagonal $AC$ at $E$, and the external bisector of angle $B$ meets line $AD$ at $F$.

Prove that the right segments $CE$ and $FM$ are parallel and congruent  if and only if $BC=2\cdot AB$."

 

Proof CiP of Original Problem 

          First of all, notice that from the equal angles:

$\angle B'BF\equiv \angle BFA$, and $\angle CBE \equiv \angle AGC$ (as angles formed by the parallel lines $BC$ and $AD$ with the transversals $BF$ and $BG$ respectively). And because the bisectors form equal angles, we have $\angle B'BF \equiv \angle FAB$, $\angle CBG \equiv \angle ABG$, so we get some isosceles triangles, from where it come

$$ AB=AF=AG\;.$$

          We will solve the original problem by the vector method.

 Denote with $L=BC,\;l=AB$. The bisector theorem $BE$ in the triangle $ABC$

$$\frac{AE}{EC}=\frac{AB}{BC}=\frac{l}{L}$$ 

allows us to find out  

$$\overrightarrow{BE}=\frac{L\cdot \overrightarrow{BA}+l\cdot \overrightarrow{BC}}{L+l}.\tag{1}$$

(Indeed, $L\cdot \overrightarrow{AE}=l\cdot \overrightarrow{EC}$, or $L(\overrightarrow{BE}-\overrightarrow{BA})=l(\overrightarrow{BC}-\overrightarrow{BE})$...)

We also obtain from the bisector theorem $AE=\frac{l}{L+l}\cdot AC$, so $\overrightarrow{AE}=\frac{l}{L+l}\overrightarrow {AC}=\frac{l}{L+l}(\overrightarrow{BC}-\overrightarrow{BA})$, hence

$$\overrightarrow {AE}=\frac{l}{L+l}\overrightarrow{BC}-\frac{l}{L+l}\overrightarrow{BA}.$$

      Further, because $AF=AB$, we have $\overrightarrow{AF}=-\frac{l}{L}\cdot \overrightarrow{AD}=-\frac{l}{L}\overrightarrow{BC}$, and now we calculate $\overrightarrow{EF}=\overrightarrow{AF}-\overrightarrow{AE}=-\frac{l}{L}\overrightarrow{BC}-(\frac{l}{L+l}\overrightarrow{BC}-\frac{l}{L+l}\overrightarrow{BA}),$ so 

$$\overrightarrow{EF}=-\frac{2Ll+l^2}{L(L+l)}\overrightarrow{BC}+\frac{l}{L+l}\overrightarrow{BA}.\tag{2}$$

 Also $\overrightarrow{CM}=\overrightarrow{BM}-\overrightarrow{BC}=\frac{1}{2}\overrightarrow{BE}-\overrightarrow{BC}\;\overset{(1)}{=}\frac{L}{2(L+l}\overrightarrow{BA}+\frac{l}{2(L+l)}\overrightarrow{BC}-\overrightarrow{BC}$, getting

$$\overrightarrow{CM}=-\frac{2L+l}{2(L+l)}\overrightarrow{BC}+\frac{L}{2(L+l)}\overrightarrow{BA}.\tag{3}$$

           From relations $(2)$ and $(3)$ we see that

$\overrightarrow{EF}=\frac{l}{L}[-\frac{2L+l}{L+l}\overrightarrow{BC}=\frac{l}{L+l}\overrightarrow{BA}]=\frac{l}{L}\cdot 2\overrightarrow{CM}$, so

$$\overrightarrow{EF}=\frac{2l}{L}\overrightarrow{CM}.\tag{4}$$

Relation $(4)$ states that  $EF\;\parallel\;CM$.

$\blacksquare$

     REMARK CiP

      Also from the formula $(4)$ we deduce that 

$EF \;\overset{\parallel}{=}\;CM\;\;\Leftrightarrow\;\;2l=L\;\;\Leftrightarrow\;\;EFMC-parallelogram\;\;\Leftrightarrow\;\;CE\;\overset{\parallel}{=}\;MF$

and we get our reformulation of the problem.

$\blacksquare\;\blacksquare$