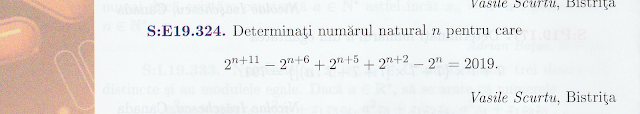Romanian Mathematical Journalin harjoitusliitteen tehtävä S:E19.323

           The problem is proposed for the 5th grade, at page 6.

 In translation (due to Miss Google):

     " Determine the natural number $n$ for which:

$$2^{n+11}-2^{n+6}+2^{n+5}+2^{n+2}-2^n=2019."$$

 

ANSWER CiP

$$n=0;$$ 

Indeed: $2^{11}-2^6+2^5+2^2-2^0= 2048-64+32+4-1=2019.$

 

 Solution CiP

           If the number $n>0$, then all the powers of $2$ on the left side of the equation are even numbers, so the result of their sum is an even number, so it cannot be equal to $2019.$

     All that remains is to check the number $n=0$, and it is found that he verifies the equation. 

$\blacksquare$

          REMARKS CiP 

          $1^R$. We will use the following formula

$$2^k\;+\;2^k\;=\;2^{k+1},\;\;\;2^{k+1}-2^k=2^k,\;\;k=0,1,2,...$$ 

          $2^R$. The number in base ten $2019$ is written in base $2$ as follows:

$2019_{(10)}=111\;1110\;0011_{(2)}$

 $\Leftrightarrow\;\;2019=2^{10}+2^9+2^8+2^7+2^6+2^5+2^1+2^0.$

As it is known, this writing is unique, there is no one like it. Replacing the terms $2^k$ with the second formula in Remark $1^R$, with the exception of $2^5$, we have:

 $2019=(2^{11}-2^{10})+(2^{10}-2^9)+(2^9-2^8)+(2^8-2^7)+(2^7-2^6)\;\underline{+2^5}\;+(2^2-2^1)+(2^1-2^0).$

 If we open all the parentheses and keep in mind that $x-y+y=x,\;\;x,y,z \in \mathbb{N}$, we get:

$2019=2^{11}-2^6+2^5+2^2-2^0.$ 

      $3^R$. The given equation can still be written, also with the formulas from the mentioned remark:

$2^{n+10}+2^{n+10}-2^{n+6}+2^{n+5}+2^{n+1}+2^{n+1}-2^n=2019$

$\Leftrightarrow\;2^{n+10}+(2^{n+10}-2^{n+9})+(2^{n+9}-2^{n+8})+(2^{n+8}-2^{n+7})+(2^{n+7}-2^{n+6})+2^{n+5}+(2^{n+2}-2^{n+1})+(2^{n+1}-2^n)=2019$

 $\Leftrightarrow\;2^{n+10}+2^{n+9}+2^{n+8}+2^{n+7}+2^{n+6}+2^{n+5}+2^{n+1}+2^n=2019,$

 and considering the unique writing in base $2$, we obtain the only possibility $n = 0.$

 $\square\;\square\;\square$

FUNDAMENTELE GEOMETRIEI EUCLIDIENE - H.G. FORDER

Harnicul Scamatorist LIVU PODGORNEI face o lucrare care nu poate fi pretuita, in scanarea unor carti de matematica din vechi timpuri.

Link-ul direct, atat cat va exista, este

 https://lookaside.fbsbx.com/file/Fundamentele%20geometriei%20euclidiene%20-%20H.G.%20Forder%20%281970%29.pdf?token=AWyaMZGCbmxaspLfivLcW3CTWs6igWfuUN_y_rzX6OVJkHHnnKahk1nUsgi0cT4Fx4mobxsHnQWWElZZ0_OhCo_HsxnZGRFjl312UgtpJ7kNM7u8HBG3NRTSnC0EboqJLe5pW5YvKzv9Z-pd4KmsW-2zaohnv3ULJdQ8XFLc8QurBqkYpuf7yXO7Srq_Xr9pzzURrZV7K8RhOMnhO-Ku91q6XwBWQy9LX59cK53wqc3mL4cOJZNVfKFx3eCwPSi6g3hCKiCqhxd8JG3H31ata_UGmYjGBdqiMMoreaIbzqDLUVmgH9oQSKRbvHrk0jS3XBqopUJl4OFf63RnjjzU7iIfmQuZnMIyJF82jbXDpbHT0A-KllTVCqyIziFTzt1osWFgYj6ZFCETbG31J9dgE_naSz74MGwjvuGibcT4XPlPeSrY7iPBng3vCrNweZ3G8Du8Yic1NO11IVNMtqWDz7yWurtyrtJVvBXD-NOqRzIB0CLI_8doYBzcHwu4j9uVLuSUG4mWaWmaosxNtE1-nM0-

 

Cartea arata "pe dinafara" asa

Succes la "explorarea pe dinauntru". 

Puteti descarca si de aici.

About the PROBLEM #2 ("икки") from International Olympiad "TUYAMAADA" 2021 - Junior League

           See link, obtained from www.molympiad.net.

          We will formulate the following related problem:

 

"The bisector of angle $B$ of a parallelogram $ABCD$ meets itd diagonal $AC$ at $E$, and the external bisector of angle $B$ meets line $AD$ at $F$.

Prove that the right segments $CE$ and $FM$ are parallel and congruent  if and only if $BC=2\cdot AB$."

 

Proof CiP of Original Problem 

          First of all, notice that from the equal angles:

$\angle B'BF\equiv \angle BFA$, and $\angle CBE \equiv \angle AGC$ (as angles formed by the parallel lines $BC$ and $AD$ with the transversals $BF$ and $BG$ respectively). And because the bisectors form equal angles, we have $\angle B'BF \equiv \angle FAB$, $\angle CBG \equiv \angle ABG$, so we get some isosceles triangles, from where it come

$$ AB=AF=AG\;.$$

          We will solve the original problem by the vector method.

 Denote with $L=BC,\;l=AB$. The bisector theorem $BE$ in the triangle $ABC$

$$\frac{AE}{EC}=\frac{AB}{BC}=\frac{l}{L}$$ 

allows us to find out  

$$\overrightarrow{BE}=\frac{L\cdot \overrightarrow{BA}+l\cdot \overrightarrow{BC}}{L+l}.\tag{1}$$

(Indeed, $L\cdot \overrightarrow{AE}=l\cdot \overrightarrow{EC}$, or $L(\overrightarrow{BE}-\overrightarrow{BA})=l(\overrightarrow{BC}-\overrightarrow{BE})$...)

We also obtain from the bisector theorem $AE=\frac{l}{L+l}\cdot AC$, so $\overrightarrow{AE}=\frac{l}{L+l}\overrightarrow {AC}=\frac{l}{L+l}(\overrightarrow{BC}-\overrightarrow{BA})$, hence

$$\overrightarrow {AE}=\frac{l}{L+l}\overrightarrow{BC}-\frac{l}{L+l}\overrightarrow{BA}.$$

      Further, because $AF=AB$, we have $\overrightarrow{AF}=-\frac{l}{L}\cdot \overrightarrow{AD}=-\frac{l}{L}\overrightarrow{BC}$, and now we calculate $\overrightarrow{EF}=\overrightarrow{AF}-\overrightarrow{AE}=-\frac{l}{L}\overrightarrow{BC}-(\frac{l}{L+l}\overrightarrow{BC}-\frac{l}{L+l}\overrightarrow{BA}),$ so 

$$\overrightarrow{EF}=-\frac{2Ll+l^2}{L(L+l)}\overrightarrow{BC}+\frac{l}{L+l}\overrightarrow{BA}.\tag{2}$$

 Also $\overrightarrow{CM}=\overrightarrow{BM}-\overrightarrow{BC}=\frac{1}{2}\overrightarrow{BE}-\overrightarrow{BC}\;\overset{(1)}{=}\frac{L}{2(L+l}\overrightarrow{BA}+\frac{l}{2(L+l)}\overrightarrow{BC}-\overrightarrow{BC}$, getting

$$\overrightarrow{CM}=-\frac{2L+l}{2(L+l)}\overrightarrow{BC}+\frac{L}{2(L+l)}\overrightarrow{BA}.\tag{3}$$

           From relations $(2)$ and $(3)$ we see that

$\overrightarrow{EF}=\frac{l}{L}[-\frac{2L+l}{L+l}\overrightarrow{BC}=\frac{l}{L+l}\overrightarrow{BA}]=\frac{l}{L}\cdot 2\overrightarrow{CM}$, so

$$\overrightarrow{EF}=\frac{2l}{L}\overrightarrow{CM}.\tag{4}$$

Relation $(4)$ states that  $EF\;\parallel\;CM$.

$\blacksquare$

     REMARK CiP

      Also from the formula $(4)$ we deduce that 

$EF \;\overset{\parallel}{=}\;CM\;\;\Leftrightarrow\;\;2l=L\;\;\Leftrightarrow\;\;EFMC-parallelogram\;\;\Leftrightarrow\;\;CE\;\overset{\parallel}{=}\;MF$

and we get our reformulation of the problem.

$\blacksquare\;\blacksquare$

 

 

 

 

 

 

 

 

 

Крайні значення раціонального дробу

           We are looking for the extreme values of some rational fractions of form 

$$\frac{Ax^2+2Bx+C}{ ax^2+2bx+c}.$$

     We find in the book Daniel SITARU - Fenomen Algebric

     PROBLEM #1, page 27

In translation (thanks to Miss Google for this):

     " Find the minimum of the expression 

$$E=\frac{4ab-11a^2-14b^2}{3(a^2+b^2)}\; ;\;a,b \in \mathbb{R^*}."$$ 

 

ANSWER CiP

           We will find out more, both the minimum and the maximum of the expression.

$$-5=E(a,-2a)\leqslant  E(a,b) \leqslant E(2b,b)=-\frac{10}{3}\;\;,a,b \in \mathbb{R^*}.$$ 

 

Solution CiP

      The  number $\lambda$ is a value of the fraction $E$ if, and only if

" there are two numbers $a$ and $b$ such that $\lambda =E(a,b)"

$$\Leftrightarrow \; \exists \;a,b \in \mathbb{R^*}\;such\; that\;\lambda =\frac{4ab-11a^2-14b^2}{3(a^2+b^2)}$$

 $$\Leftrightarrow\;\exists\;a,b \in \mathbb{R^*}\;such\;that\;4ab-11a^2-14b^2=3\lambda a^2+3 \lambda b^2$$

 $$\Leftrightarrow\;\exists\;a,b \in \mathbb{R^*}\;such\;that\;(3\lambda+11)a^2-4ab+(3\lambda+14)b^2=0$$

$$\Leftrightarrow\; t=\frac{a}{b}\;is\;a\;root\;of\;the\;equation\;(3\lambda+11)t^2-4t+(3\lambda+14)=0 \tag{1}$$

$\Leftrightarrow\;\Delta _t\;\geqslant 0,\tag{2}$

where $\Delta _t$ is the half-discriminant to the equation (1),

$\Delta _t=4-(3\lambda+11)(3\lambda+14).$

But $(2)\;\Leftrightarrow\;9\lambda ^2+75 \lambda+150 \leqslant 0\;\Leftrightarrow\;3\lambda^2+25\lambda+50\leqslant 0\;\Leftrightarrow\;\lambda \in [-5;-\frac{10}{3}]$.

Here, the ends of the range $[-5;-\frac{10}{3}]$ are the roots of the equation $3\lambda^2+25\lambda+50=0.$

           Result that we have  $\lambda _{min}=-5,\;\lambda _{max}=-\frac{10}{3}.$

Further, 

$E(a,b)=-5\;\Leftrightarrow\;-4a^2-4ab-b^2=0\;\Leftrightarrow\;-(2a+b)^2=0\;\Leftrightarrow\;b=-2a$,

 and $E(a,b)=-\frac{10}{3}\;\Leftrightarrow\;a^2-4ab+4b^2=0\;\Leftrightarrow\;(a-2b)^2=0\;\Leftrightarrow\;a=2b.$

 We got the answer.

$\blacksquare$

 

Solution #2

(the authors' solution, only for the minimum, completed by CiP for the maximum)

 See page 72.

           Completed by CiP: $E=\frac{-10a^2-10b^2-a^2+4ab-4b^2}{3(a^2+b^2)}=-\frac{10}{3}-\frac{(a-2b)^2}{3(a^2+b^2)}\leqslant -\frac{10}{3}$,  $max\;E=-\frac{10}{3}$ for $a-2b=0.$

$\blacksquare$

 

GAZETA MATEMATICĂ Seria B N0 1/2022

vezi in DRIVE

Vezi ERATA

 

 
 

 

 

SUPLIMENTUL cu EXERCIȚII al GMB N0 1/2022

vezi in DRIVE
 

 

 

Karede Bir Açı ve Bir ... Hiçbir Yerden Uçurtma

           An Angle in a Square and a Kite Out of Nowhere

          Uçurtma, akademik dilde Deltoid olarak da adlandırılır.

          Starting from a geometry problem and the solution that Hasan Ata offered, we formulate the following problem:

          " Let $ABCD$ be a square and an angle $\angle EAF$ with $E \in ]BC[,\;F \in ]CD[$. Prove that 

$$\measuredangle EAF=45^{\circ}\;\Leftrightarrow\;EF=BE+DF."$$

Solution CiP

                    Let $\measuredangle EAF=45^{\circ}$

               Rotate the triangle $ABE$ with  $90^{\circ}$ clockwise around point $A$ and obtain the triangle $ADG$. We have $\measuredangle EAG=90^{\circ}$, $AE=AG$ and $DG=BE$.

  Since $\measuredangle FAG=90^{\circ}-45^{\circ}=45^{\circ}=\measuredangle EAF$ , it follows that the line $AF$  is the angle bisector of the $\angle EAG$ in the isosceles triangle $AEG$ so it is the perpendicular bisector of the segment $[EG]$, hence $FG=FE$, so $EF=FG=DG+DE=BE+DF$.

q.e.d.

           Reciprocally, let $EF=BE+DF$

       The same rotation now shows us that $FG=FE$ so quadrilateral $AEFG$ is a kite.

  Hence line $FA$ is simultaneously angle bisector of $\angle EFG$ and $\angle EAG$. Because $\measuredangle EAG=90^{\circ}$ it follow $\measuredangle EAF=\frac{90^{\circ}}{2}=45^{\circ}.$ 

q.e.d.

$\blacksquare$